Image Reconstruction with Predictive Filter Flow(PFF)

---

Paper

Abstract: Non-uniform motion blur removal, lossy compression artifact reduction, single image SR

• Filter Flow: Pixels in a local neighborhood of the input image are linearly combined to reconstruct pixel at the same location.(like convolution) BUT filter weights changes one spatial location to the next.

  Filter Flow Paper

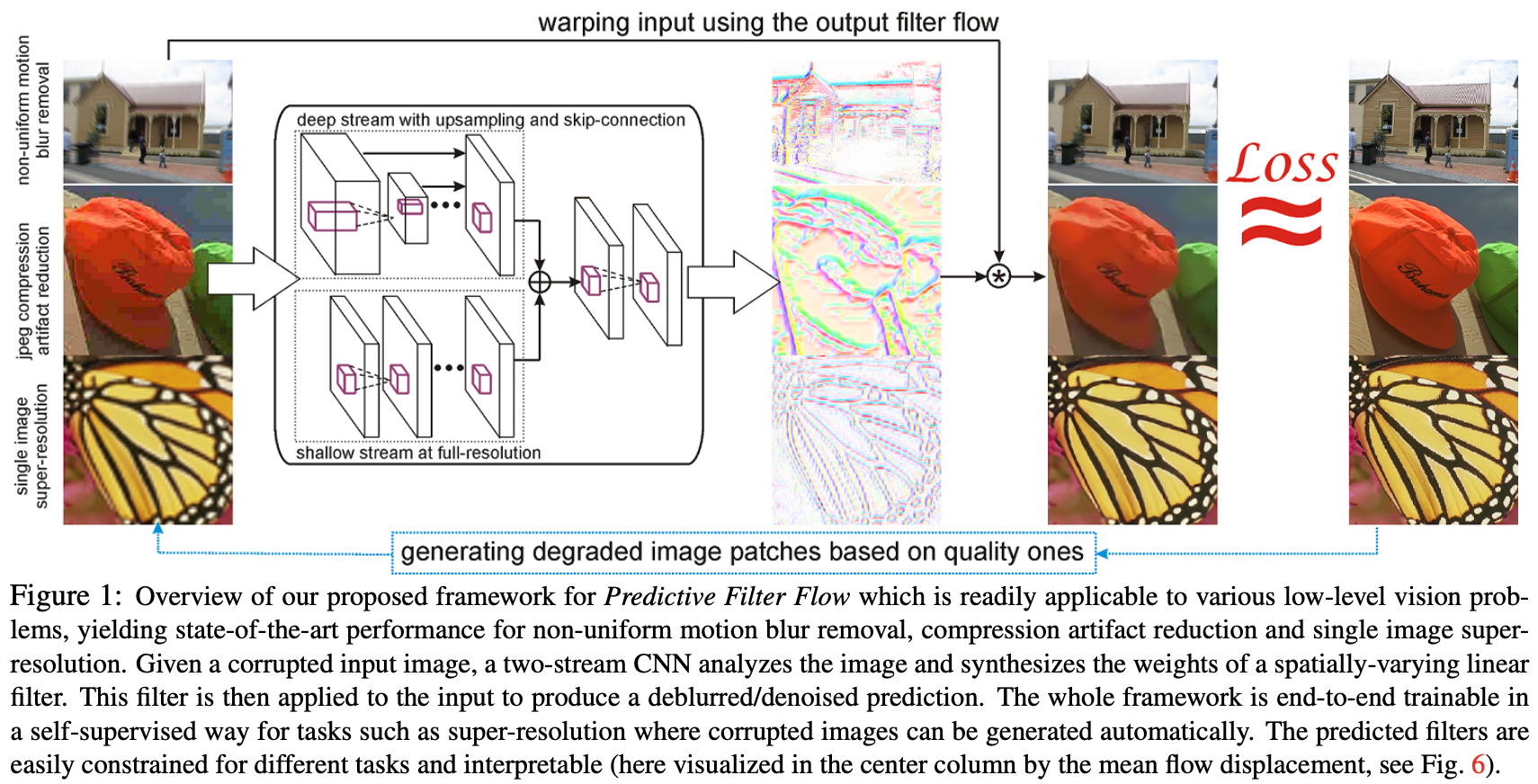
Fig.1: PFF algorithm overview

1. The method is controllable( the results can be estimated , in CNN based methods the result of an input image that is not in the training and testing set cannot be estimated). Output image can be analyzed how the constructed image is generated.

2. End-to-end trainable

$$I_2 = TI_1 \qquad T \in \Gamma$$

$$ {I_2: Output\ image
I_1: Input\ image
T: model\ in\ \Gamma
\Gamma: Constraint\ Space}

• Instead of optimizing over $T$ directly, learn $T$ from data: $I_2 \approx \hat{T}I_1, \quad \hat{T} = f_w(I_1)$

  Data pairs –> ${(I_1^i, I_2^i)}$ \ Define loss function between them to find $f_w(.)$ $loss^i = \ell(I_2^i - f_w(I_1^i)I_1^i)$$ any loss function($L_1\,norm$ in this paper)\ Also, regularization term defined as: $R(f_w(I_1^i))$ used $L_2 \, regularization$

  $$\underbrace{min}_{w}(\sum_{i=1}^N (\,loss^i + R(f_w(I_1^i)) \,)$$

• Architecture: Network only includes convolutional layers. One path includes dense layers with pooling(resolution decreases), second path includes shallow layers(with full resolution). At the end of these paths, feature maps combined and a final convolution layer added. The result of the network gives filter flow. Then, filter flow is convolved with input image and SR image generated.\

  1. Training:
     • Original High resolution image degrading to inverse scale (if $4x$ upscale is desired, image downsampled $\frac{1}{4} x$)
     • Downsampled image is upscaled using bicubic interpolation with anti-alising
     • Network output gives filter flow.
     • Filter flow is applied to input image and final result obtained.
     • Loss is calculated above loss function calculation and network weights updated with back-propagation.
  2. Inference:
     • Filter flow($I_2 = f_w(Input Image)$) is calculated from input image.
     • $I_{SR} = I_{Input} * I_2$ (Filter Flow is applied to input image)